Q1. [Maximum mark: 24]
(a) (i) Use trigonometric ratios to prove that in a triangle ABC
.
(ii) Prove that the area of the triangle is .
(iii) Given that R denotes the radius of the circumscribed circle prove that .
(iv) Hence show that the area of the triangle ABC is .
(b) A new triangle DEF is positioned within a circle radius R such that DF is a diameter as shown in the following diagram.
(i) Find in terms of R, the two values of (DE)2 such that the area of the shaded region is twice the area of the triangle DEF.
(ii) Using two diagrams, explain why there are two values of (DE)2 .
(c) A parallelogram is positioned inside a circle such that all four vertices lie on the circle. Prove that it is a rectangle.
Q2. [Maximum mark: 14]
(a) Figure 1 shows a tangent [PQ] at the point Q of a circle and a line [PS] meeting the circle at the points R , S and passing through the centre O of the circle. Show that PQ2 = PR × PS .
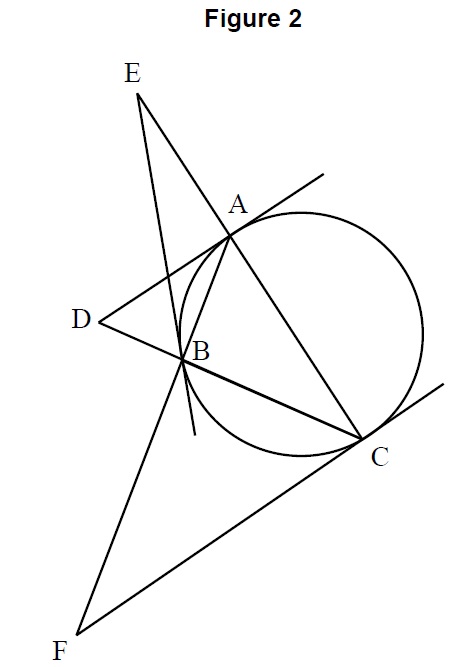
(b) Figure 2 shows a triangle ABC inscribed in a circle. The tangents at the points A , B , C meet the opposite sides of the triangle externally at the points D , E , F respectively.
(i) Show that
.
(ii) By considering a pair of similar triangles, show that
and hence that
.
(iii) By writing down and using two further similar expressions, show that the points D , E , F are collinear.
Q3. [Maximum mark: 15]

Q4. [Maximum mark: 15]

Q5. [Maximum mark: 15]

Q6. [Maximum mark: 15]




