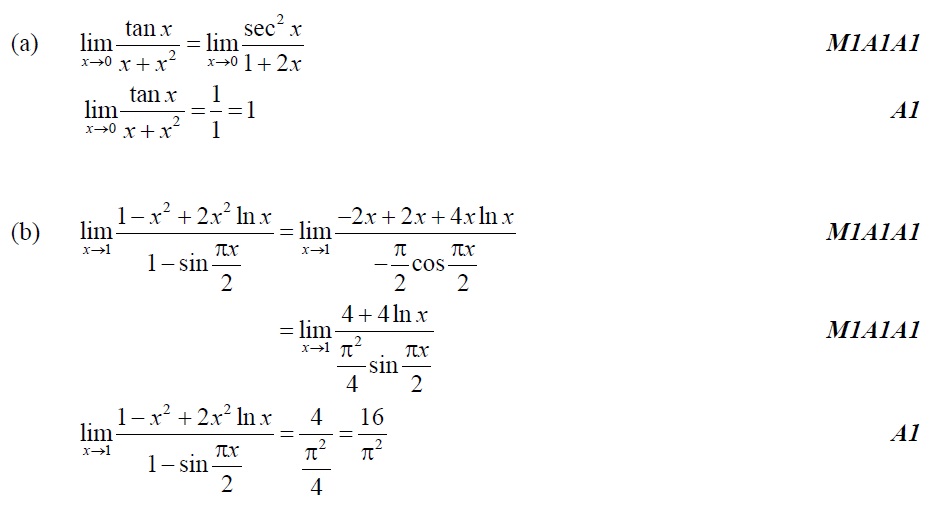IBDP Past Year Exam Questions – Limits
1. [N18/P3/TZ0]
(a) Use L’Hôpital’s rule to determine the value of . [5 marks]
(b) Hence find . [3 marks]
2. [M17/P3/TZ0]
Use l’Hôpital’s rule to determine the value of . [7 marks]
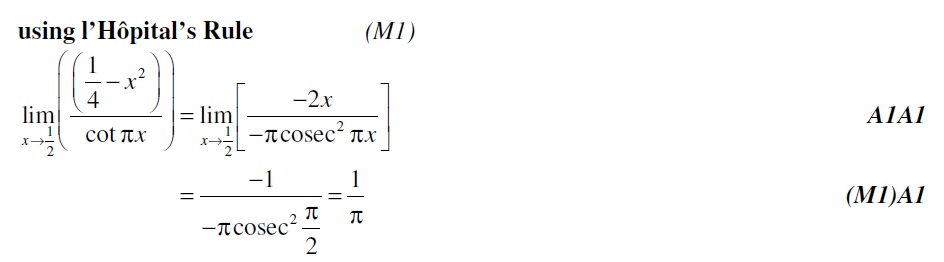
3. [N16/P3/TZ0]
Using l’Hôpital’s rule, find . [6 marks]
4. [M16/P3/TZ0]
Determine the exact value of . [3 marks]
5. [M16/P3/TZ0]
Use l’Hôpital’s rule to find . [4 marks]
6. [M17]
Using l’Hôpital’s rule, show that where . [4 marks]
7. [M16]
Use l’Hôpital’s rule to show that . [3 marks]
8. [M14]
Using l’Hôpital’s rule, show that .
9. [M11/P3/TZ0]
(a) Find the first three terms of the Maclaurin series for
. [6 marks]
(b) Hence, or otherwise, determine the value of
. [4 marks]
10. [N11/P3/TZ0]
Find
11. [M09/P3/TZ0]
Find
(i) ; [4 marks]
(ii) . [7 marks]
12. [N10/P3/TZ0]
Find . [7 marks]