Practice – Non Right-Angled Triangle Trigonometry
1. The sides of a triangle are in arithmetic sequence and the greatest angle is double the smallest angle. Prove that the ratio of its sides is 4:5:6.
2. If , prove that is either isosceles, or right angled.
3. The angles of a triangle are in the ratio 1:2:7, then show that the ratio of the greatest side to the least side is .
4. If the angles of a triangle are and and the included side is cm, the area of the triangle is cm2.
5. The sides of a triangle are then find the value of the greatest angle of the triangle.
6. The diagram shows a sector of a circle OAB. C is the midpoint of OB. Angle AOB is radians.
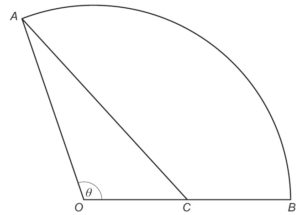
Given that the area of the triangle OAC is equal to one quarter of the area of the sector OAB, show that . [4 marks]
7.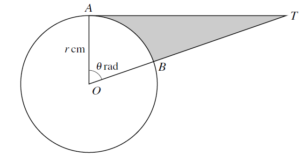
The diagram shows a circle with centre O and radius
cm. The points A and B lie on the circle and AT is a tangent to the circle. Angle AOB = 1 radians and OBT is a straight line.
(i) Express the area of the shaded region in terms of
and
. [3 marks]
(ii) In the case where and , find the perimeter of the shaded region. [4 marks]
