Practice Questions – Complex Numbers

Q1. The complex numbers  $z_1$ and  $z_2$ are given by  $z_1=\sqrt{2}+\sqrt{2}i$ and  $z_2=\sqrt{3}–i$

(i) Find the modulus and argument of each of  $z_1$ and  $z_2$ .  [6 marks]
(ii) Plot the points representing each of $z_1$ ,  $z_2$ and  $z_1+z_2$ on an Argand diagram. [3 marks]
(iii) Hence find the exact value of  $\tan \frac{\mathrm{\pi }}{24}$ . [5 marks]

Q2. 

Q3. 

Q4. 

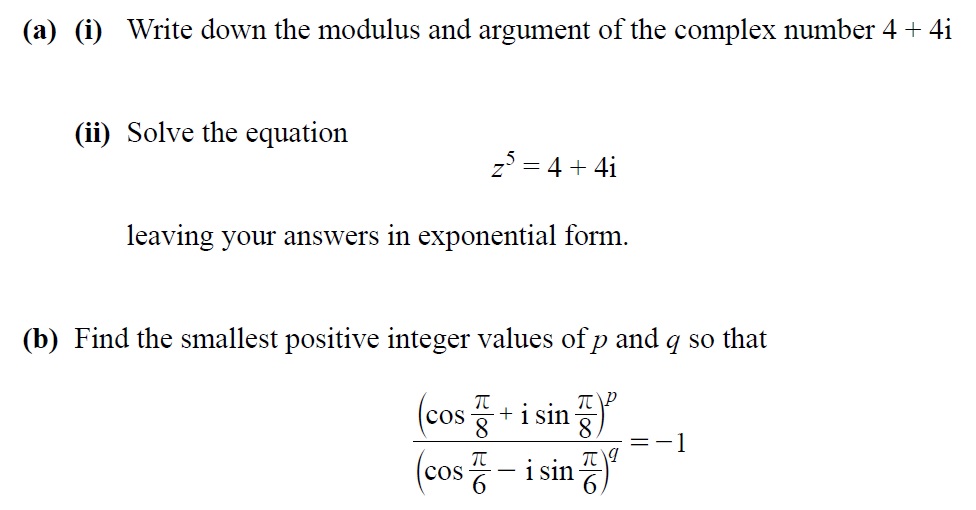
Q5.

Q6. (i) The complex number  $z$ is such that $z^2=1+i\sqrt{3}$ . Find the two possible values of  in the forma $a+ib$ , where  $a$ and $b$ are exact real numbers. [5 marks]
(ii) With the value of  $z$ from part (i)such that the real part of $z$ is positive, show on an Argand diagram the points A and B representing  $z$ and $z^2$ respectively. [2 marks]
(iii) Specify two transformations which together map the line segment OA to the line segment OB, where O is the origin. [4 marks]

Q7.