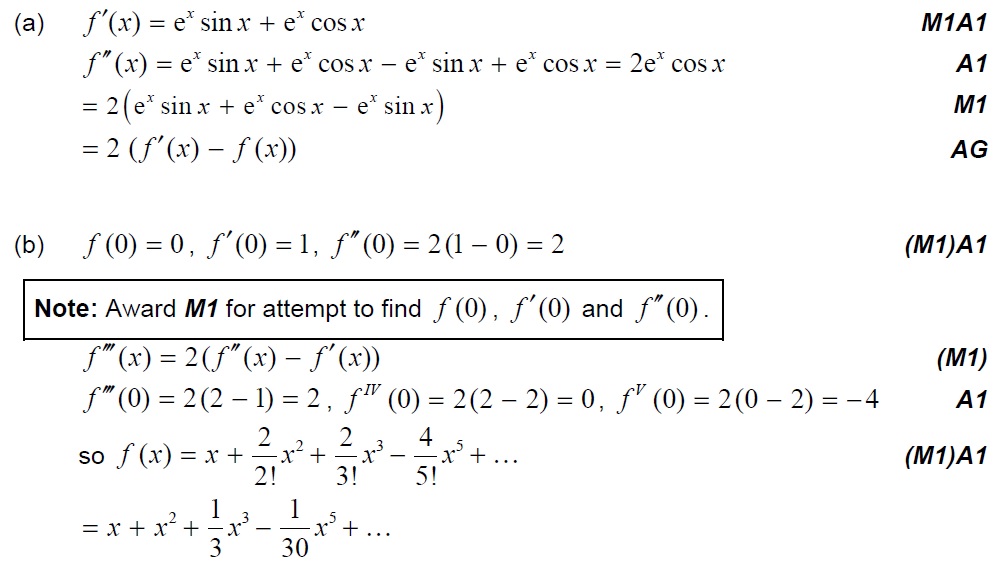IBDP Past Year Exam Papers – Maclauren Series

1. [M17/P3/TZ0]

Let the Maclaurin series for $\tan x$ be  $\tan x= a_{1}x + a_3{x}^3 + a_5{x}^5 + ......$ where  $a_1 , a_3$ and  $a_5$ are constants.

(a) Find series for  $se{c}^2 x$ , in terms of  $a_1 , a_3$ and  $a_5$ , up to and including the  $x^4$ term

(i) by differentiating the above series for  $\tan x$ ;
(ii) by using the relationship  $se{c}^2 x= 2 + {\tan }^2 x$ .   [3 marks]

(b) Hence, by comparing your two series, determine the values of  $a_1 , a_3$ and  $a_5$ .   [3 marks]

2. [N16/P3/TZ0]

(a) By successive differentiation find the first four non-zero terms in the Maclaurin series for $f\left(x\right)=\left(x+1\right)\ln \left(1+x\right) – x$ . [11 marks]

(b) Deduce that, for n ≥ 2 , the coefficient of  $x^n$ in this series is  ${\left(–1\right)}^n\frac{1}{n\left(n–1\right)}$ .   [1 mark]

3. [M16]

Consider the functions  $f_n\left(x\right)=se{c}^n\left(x\right), \left|x\right|<\frac{\mathrm{\pi }}{2}$ and  $g_n\left(x\right)=f_n\left(x\right)\tan x$ .

(a)        Show that

           (i)  $\frac{d{f}_n\left(x\right)}{dx}=n{g}_n\left(x\right);$

          (ii)   $\frac{d{g}_n\left(x\right)}{dx}=\left(n+1\right)f_{n+2}\left(x\right)–n{f}_n\left(x\right)$ .    [5 marks]

(b)     (i)   Use these results to show that the Maclauren series for the function  $f_5\left(x\right)$ up to and including the term in  $x^4$ is  $1+\frac{5}{2}{x}^2+\frac{85}{24}{x}^4$ .

        (ii)   By considering the general form of its higher derivatives explain briefly why all coefficients in the Maclauren series for the function $f_5\left(x\right)$ are either positive or zero.

       (iii)   Hence show that  $se{c}^3\left(0.1\right)>1.02535$ .    [14 marks]

4. [N15/P3/TZ0]

Let  $f\left(x\right)=e^x\sin x$ .

(a) Show that  $f‘‘\left(x\right)=2\left(f‘\left(x\right)–f\left(x\right)\right)$ .   [4 marks]

(b) By further differentiation of the result in part (a) , find the Maclaurin expansion of  $f\left(x\right)$  , as far as the term in  $x^5$ .  [6 marks]

5. [M15/P3/TZ0]

The function $f$ is defined by $f\left(x\right)=e^{–x}\cos x + x – 1$ .

By finding a suitable number of derivatives of  $f$ , determine the first non-zero term in its Maclaurin series.   [7 marks]

6. [M09/P3/TZ0]

The variables $x$ and  $y$ are related by  $\frac{dx}{dy} – y\tan x=\cos x$ .
(a) Find the Maclaurin series for  $y$ up to and including the term in $x^2$ given that when  $x=0$ . [7 marks]
(b) Solve the differential equation given that  $y=0$ when  $x=\mathrm{\pi }$ . Give the solution in the form  $y=f\left(x\right)$ . [10 marks]

7. [N09/P3/TZ0]

The function  $f$ is defined by  $f\left(x\right)=e^{\left(e^x–1\right)}$ .

(a) Assuming the Maclaurin series for  $e^x$ , show that the Maclaurin series for  $f\left(x\right)$ is  $1 + x +x^2 + \frac{5}{6}{x}^3 +........$ [5 marks]

(b) Hence or otherwise find the value of  $\underset{x\to 0}{lim}\frac{f\left(x\right) – 1}{f‘\left(x\right) – 1}$ .  [5 marks]

8. [M10/P3/TZ0]

(a) Using the Maclaurin series for  ${\left(1+x\right)}^n$ , write down and simplify the Maclaurin series approximation for ${\left(1–x^2\right)}^{\frac{1}{2}}$ as far as the term in  $x^4$ . [3 marks]

(b) Use your result to show that a series approximation for arccos  $x$ is arccos  $x\approx \frac{\mathrm{\pi }}{2} – x – \frac{1}{6}{x}^3 – \frac{3}{40}{x}^5$ .    [3 marks]

(c) Evaluate  $\underset{x\to 0}{lim}\frac{{\displaystyle \frac{\mathrm{\pi }}{2}}–arc\cos \left(x^2\right) – x^2}{x^6}$ .   [5 marks]

(d) Use the series approximation for arccos  $x$ to find an approximate value for                                     

                                      ${\int }_0^{0.2}arc\cos \left(\sqrt{x}\right)dx$ ,    

giving your answer to 5 decimal places. Does your answer give the actual value of the integral to 5 decimal places?    [6 marks]

9. [N10/P3/TZ0]

(a) Using the Maclaurin series for the function ex , write down the first four terms of the Maclaurin series for   $e^{– \frac{x^2}{2}}$ .   [3 marks]

(b) Hence find the first four terms of the series for  ${\int }_0^x{e}^{– \frac{u^2}{2}}du$ .  [3 marks]

(c) Use the result from part (b) to find an approximate value for   $\frac{1}{\sqrt{2\mathrm{\pi }}}{\int }_0^1{e}^{– \frac{x^2}{2}}dx$ .    [3 marks]