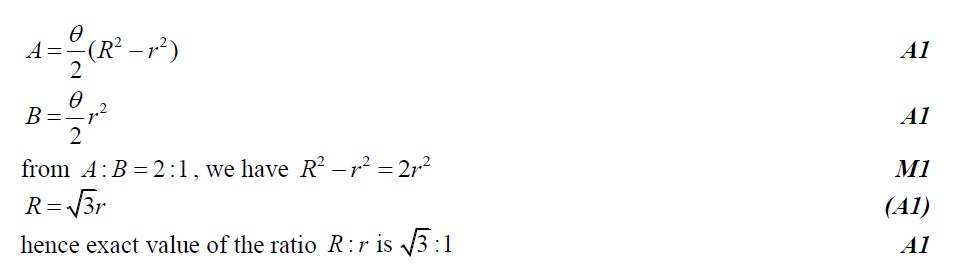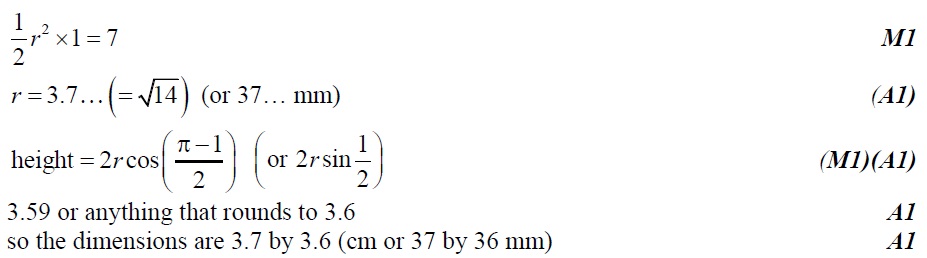IBDP Past year Exam Questions – Circular measure

Q1.   [M09.P1.TZ1]

The diagram below shows two straight lines intersecting at O and two circles, each with centre O. The outer circle has radius R and the inner circle has radius r .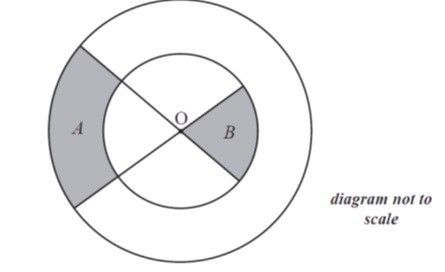

Consider the shaded regions with areas A and B . Given that A: B = 2 :1, find the exact value of the ratio R : r .        [5 marks]   

Q2.  [N09.P2]

The diagram below shows two concentric circles with centre O and radii 2 cm and 4 cm. The points P and Q lie on the larger circle and  $P\hat{O}Q=x$ , where $0<x<\frac{\mathrm{\pi }}{2}$ .     

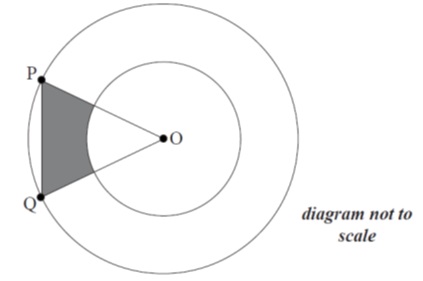
(a) Show that the area of the shaded region is $8 \sin x–2x$ .    [3 marks]   

(b) Find the maximum area of the shaded region.    [4 marks]

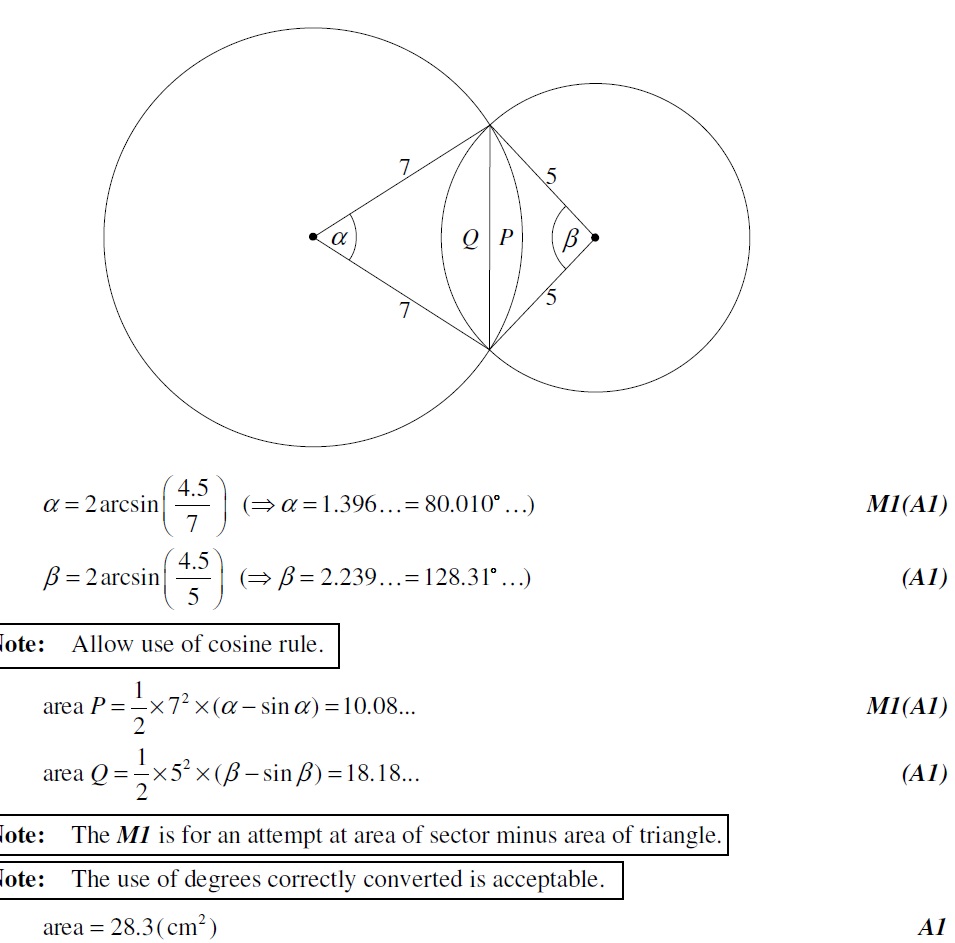
Q3.   [M11.P2.TZ1]

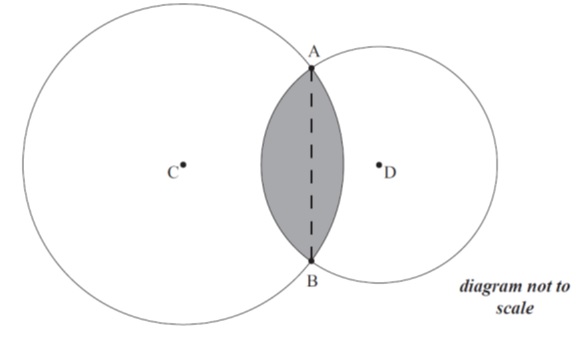
The radius of the circle with centre C is 7 cm and the radius of the circle with centre D is 5 cm. If the length of the chord [AB] is 9 cm, find the area of the shaded region enclosed by the two arcs AB.  [7 marks]

Q4.   [M12/P2/TZ2]

Two discs, one of radius 8 cm and one of radius 5 cm, are placed such that they touch each other. A piece of string is wrapped around the discs. This is shown in the diagram below.

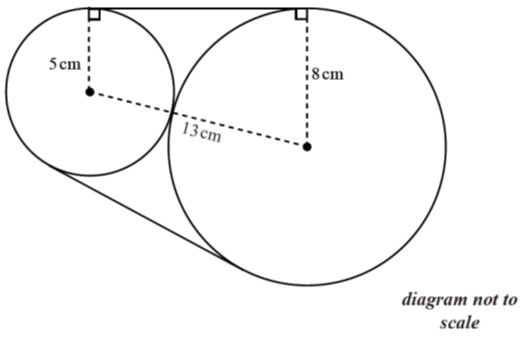
Calculate the length of string needed to go around the discs.  [8 marks]

Q5.   [N13/P2]

The diagram below shows a semi-circle of diameter 20 cm, centre O and two points A and B such that  $A\hat{O}B=\theta$ , where θ is in radians.

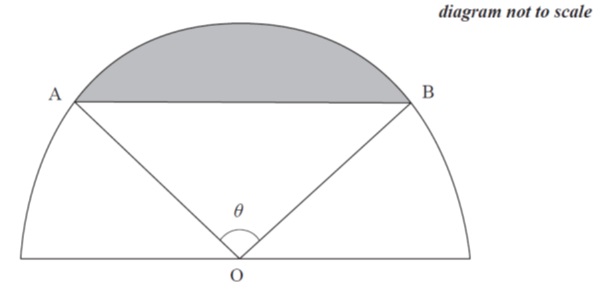
(a) Show that the shaded area can be expressed as  $50\theta –50\sin \theta$ .      [2marks]                            

(b) Find the value of θ for which the shaded area is equal to half that of the unshaded area, giving your answer correct to four significant figures.    [3 marks]

Q6.   [M13/P2/TZ2]

A circle of radius 4 cm , centre O , is cut by a chord [AB] of length 6 cm.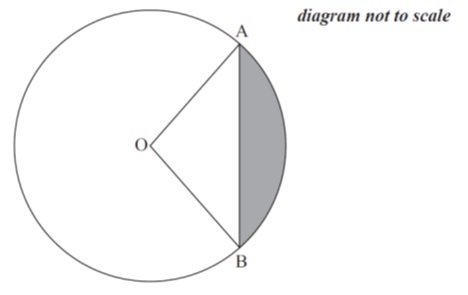  

(a) Find , expressing your answer in radians correct to four significant figures.                  [2 marks]

(b) Determine the area of the shaded region.    [3 marks]

Q7.   [M13/P2/TZ1]

A rectangle is drawn around a sector of a circle as shown. If the angle of the sector is 1 radian and the area of the sector is , find the dimensions of the rectangle, giving your answers to the nearest millimetre.         

Q8.   [M11/P2/TZ2]

The points P and Q lie on a circle, with centre O and radius 8 cm, such that  $P\hat{O}Q={59}^{\circ }$ .

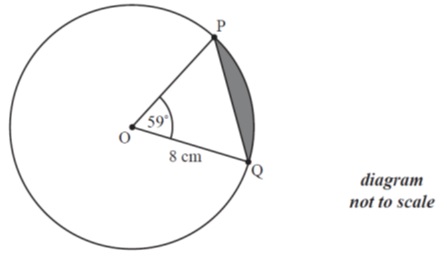
Find the area of the shaded segment of the circle contained between the arc PQ and the chord [PQ].

Q9.   [M14/P2/TZ2]

The following diagram shows two intersecting circles of radii 4 cm and 3 cm. The centre C of the smaller circle lies on the circumference of the bigger circle. O is the centre of the bigger circle and the two circles intersect at points A and B.

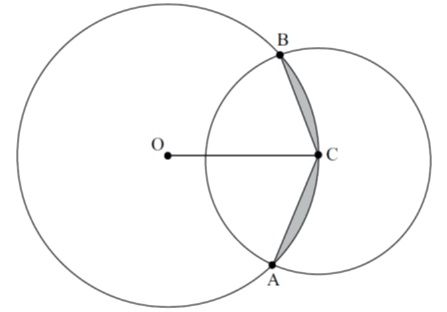
Find:       (a)   $B\hat{O}C$ ;      [2 marks]                                                           

               (b) the area of the shaded region.              [4 marks]     

Q10.   [M11/P1/TZ2]

The diagram shows a tangent, (TP) , to the circle with centre O and radius r . The size of is θ radians.

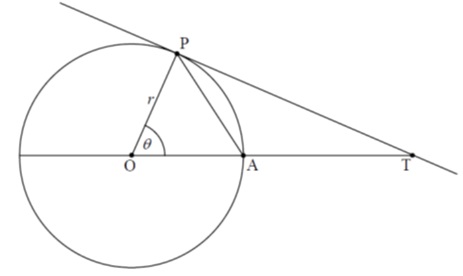
(a) Find the area of triangle AOP in terms of r and θ .         [1 mark]      

(b) Find the area of triangle POT in terms of r and θ .        [2 marks]     

(c) Using your results from part (a) and part (b), show that $\sin \theta <\theta <\tan \theta$ . [2 marks] 

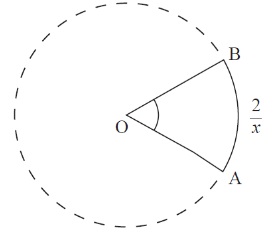
Q11.   [N11/P1]

From a vertex of an equilateral triangle of side 2x , a circular arc is drawn to divide the triangle into two regions, as shown in the diagram below.

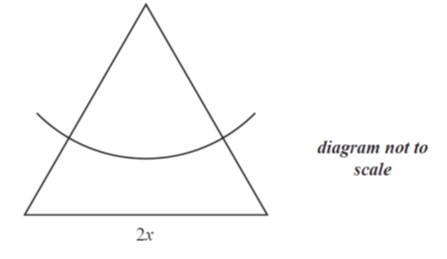
Given that the areas of the two regions are equal, find the radius of the arc in terms of x .       [6 marks]

Q12.   [N15/P1]

The following diagram shows a sector of a circle where AÔB = $x$ radians and the length of the arc AB = $2x$ cm .

Given that the area of the sector is $16c{m}^2$ , find the length of the arc AB.   [4 marks]