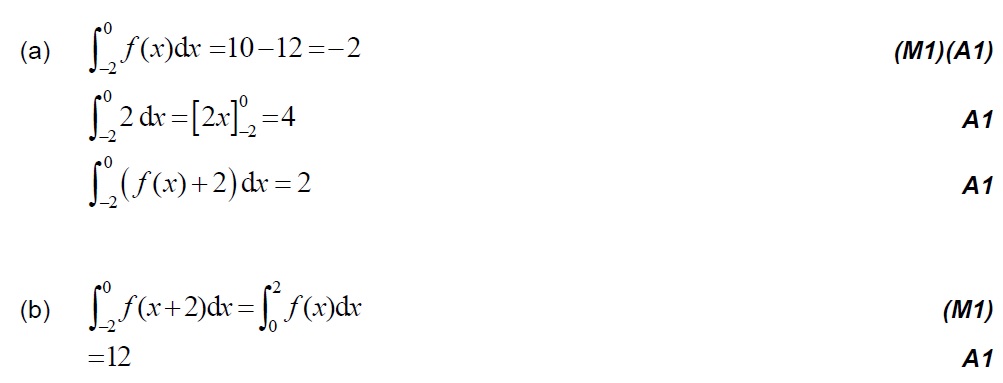IBDP Past Year Exam Questions – Definite Integrals

1.   [M18/P1/TZ1]

Given that  ${\int }_{–2}^{2}f\left(x\right)dx=10$ and  ${\int }_0^{2}f\left(x\right)dx=12$ , find

(a)  ${\int }_{–2}^{0}f\left(\left(x\right)+2\right)dx$ ;     (b)   ${\int }_{–2}^{0}f\left(x+2\right)dx$ .    [6 marks]

2.   [M18/P1/TZ2]

(a)  Use the substitution  $u=x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ to find  $\int \frac{dx}{x^{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+x^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}$ .

(b)  Hence find the value of  $\frac{1}{2}{\int }_1^9\frac{dx}{x^{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+x^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}$ , expressing your answer in the form of arctan $q$ , where  $q\in \mathrm{\mathbb{Q}}$ .                                   [7 marks]

3.   [M17/P1/TZ2]

(a)   Using the substitution $x=\tan \theta$ show that  ${\int }_0^1\frac{1}{{\left(x^2+1\right)}^2}dx={\int }_0^{\raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}{\cos }^2\theta d\theta$

(b)   Hence find the value of   ${\int }_0^1\frac{1}{{\left(x^2+1\right)}^2}dx$ .       [7 marks]

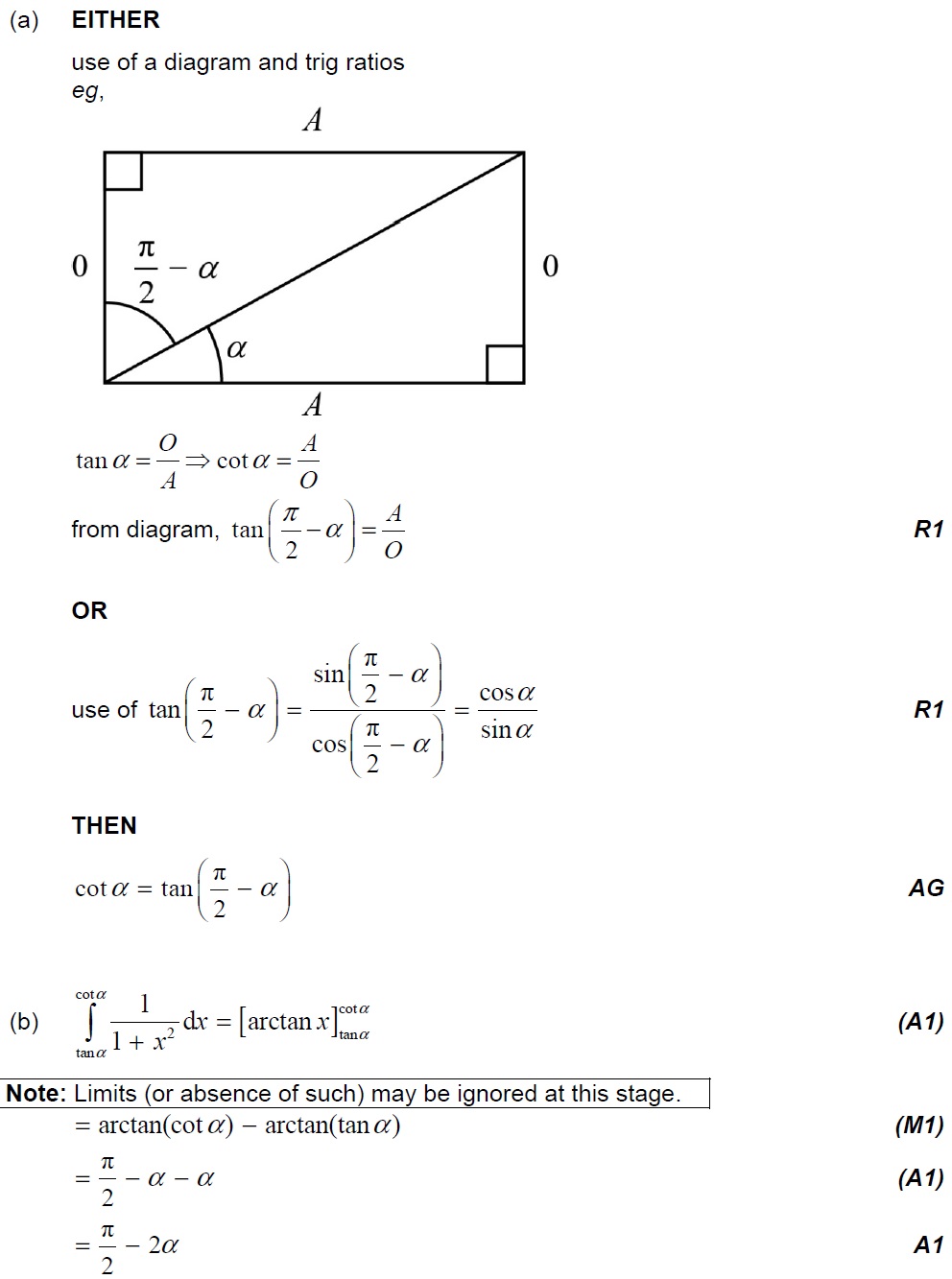
4.   [M16/P1/TZ2]

(a)  Show that  $cot \alpha =\tan \left(\frac{\pi }{2}–\alpha \right)$ for  $0<\alpha <\frac{\mathrm{\pi }}{2}$ .

(b)   Hence find  ${\int }_{\tan \alpha }^{cot\alpha }\frac{1}{1+x^2}dx , 0<\alpha <\frac{\mathrm{\pi }}{2}$ .              [5 marks]

5.   [M15/P1/TZ2]

Show that  ${\int }_1^2{x}^3\ln xdx=4\ln 2–\frac{15}{16}$ .

6.   [N99/P1]

Find the real number  $k>1$ for which  ${\int }_1^k\left(1+\frac{1}{x^2}\right)dx=\frac{3}{2}$ .