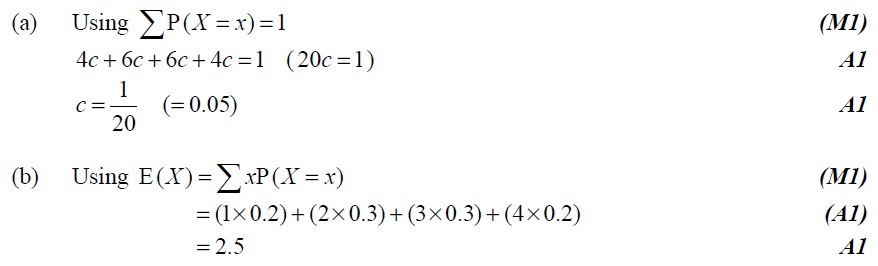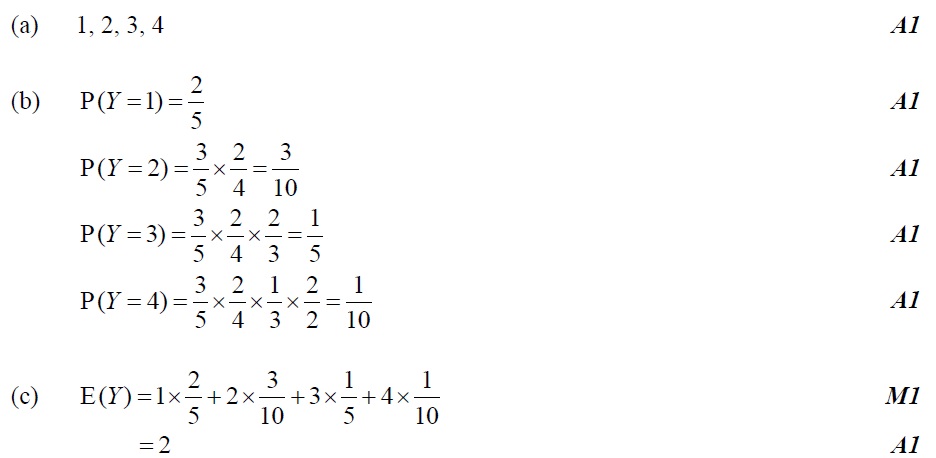IBDP Past Year Exam Questions – Discrete Random Variables

1. [M08/P1/TZ2]

The probability distribution of a discrete random variable X is defined by

$P(X=x)=cx(5–x), x=1, 2, 3, 4.$

(a)   Find the value of $c$ .   [3 marks]

(b)   Find  $E\left(X\right)$ .  [3 marks]

2. [M08/P2/TZ2]

Over a one month period, Ava and Sven play a total of n games of tennis. The probability that Ava wins any game is 0.4. The result of each game played is independent of any other game played.
Let X denote the number of games won by Ava over a one month period.
(a) Find an expression for P(X = 2) in terms of n.   [3 marks]
(b) If the probability that Ava wins two games is 0.121 correct to three
decimal places, find the value of n.   [3 marks]

3. [N08/P1/TZ0]

John removes the labels from three cans of tomato soup and two cans of chicken soup in order to enter a competition, and puts the cans away. He then discovers that the cans are identical, so that he cannot distinguish between cans of tomato soup and chicken soup. Some weeks later he decides to have a can of chicken soup for lunch.
He opens the cans at random until he opens a can of chicken soup. Let Y denote the number of cans he opens. Find
(a) the possible values of Y ,   [1 mark]
(b) the probability of each of these values of Y ,   [4 marks]
(c) the expected value of Y .   [2 marks]

4. [M99/P1]

A biased die with four faces is used in a game. A player pays 10 counters to roll the die. The table below shows the possible scores on the die, the probability of each score and the number of counters the player receives in return for each score.

Find the value of  n in order for the player to get an expected return of 9 counters per poll.   [4 marks]

5. [M10/P1/TZ2]

A biased coin is weighted such that the probability of obtaining a head is  $\frac{4}{7}$ . The coin is tossed 6 times and X denotes the number of heads observed. Find the value of the ratio  $\frac{P\left(X=3\right)}{P\left(X=2\right)}$ .

6. [M13/P1/TZ1]

7. [N13/P1/TZ0]

The discrete random variable X has probability distribution:

(a) Find the value of a .    [1]
(b) Find E(X ) .               [2]
(c) Find Var (X ) .            [3]

8. [M16/P1/TZ2]

A biased coin is tossed five times. The probability of obtaining a head in any one throw is p .
Let X be the number of heads obtained.

(a) Find, in terms of  $p$ , an expression for P(X = 4) .   [2 marks]

(b)    (i) Determine the value of  $p$ for which P(X = 4) is a maximum.
        (ii) For this value of $p$ , determine the expected number of heads. [6 marks]

9. [N17/P1/TZ0]

10. [M14/P1/TZ2]

In a pack of seven transistors, three are found to be defective. Three transistors are selected from the pack at random without replacement. The discrete random variable X represents the number of defective transistors selected.

(i) Find  $P\left(X=2\right)$ .
(ii) Copy and complete the following table:

(iii) Determine  $E\left(X\right)$ .    [6]