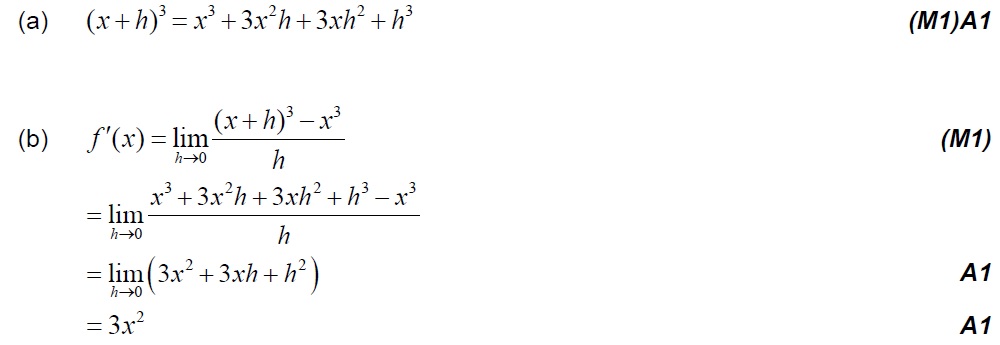IBDP Past Year Exam Questions – Introduction to Differential Calculus

1. [M15/P1/TZ1]

(a) Expand (x + h)³ .   [2 marks]
(b) Hence find the derivative of f (x) = x³ from first principles.   [3 marks]

2. [M16/P1/TZ2]

The function  $f$ is defined as $f\left(x\right)=a{x}^2+bx+c$ where  $a, b, c\in \mathrm{ℝ}$ .
Hayley conjectures that  $\frac{f\left(x_2\right)–f\left(x_1\right)}{x_2–x_1}=\frac{f‘\left(x_2\right)+f‘\left(x_1\right)}{2}, x_2\ne x_1$

Show that Hayley’s conjecture is correct.   [6 marks]

3. [M12/P1/TZ2]

Using the definition of a derivative as  $f‘\left(x\right)=\underset{}{\underset{h\to 0}{lim}\left(\frac{f\left(x+h\right)–f\left(x\right)}{h}\right)}$ , show that the derivative of $\frac{1}{2x+1}$ is $\frac{–2}{{\left(2x+1\right)}^2}$ .             [4 marks]

 

4. [N18/P2/TZ0]

Differentiate from first principles the function  $f\left(x\right)=3x^3–x$ .   [5 marks]