Notes – Quadratics

Roots of the equation  $a{x}^2+bx+c=0$

Multiplying the equation  $a{x}^2+bx+c=0$   both sides by  $4a$ , we get

$4a^2{x}^2+4abx=–4ac$

Adding  $b^2$  to both sides

$4a^2{x}^2+4abx+b^2=b^2–4ac$

${\left(2ax+b\right)}^2=b^2–4ac$

$2ax+b=\pm \sqrt{b^2–4ac}$

$x=\frac{–b \pm \sqrt{b^2–4ac}}{2a}$

Sum and Product of the roots:

If  $\alpha$  and  $\beta$  are the two roots of the above equation, then

$\alpha =\frac{–b+\sqrt{b^2–4ac}}{2a},$    $\beta =\frac{–b\pm \sqrt{b^2–4ac}}{2a}$

Adding the above two, 

Sum of the roots =  $\alpha +\beta =\frac{–b+\sqrt{b^2–4ac} –b–\sqrt{b^2–4ac}}{2a}$ $=\frac{–2b}{2a}=–\frac{b}{a}$

Product of the roots:

$\alpha \beta =\frac{{\left(–b\right)}^2–{\left[\sqrt{b^2–4ac}\right]}^2}{4a^2}$   $=\frac{b^2–b^2+4ac}{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}$

Nature of the roots:

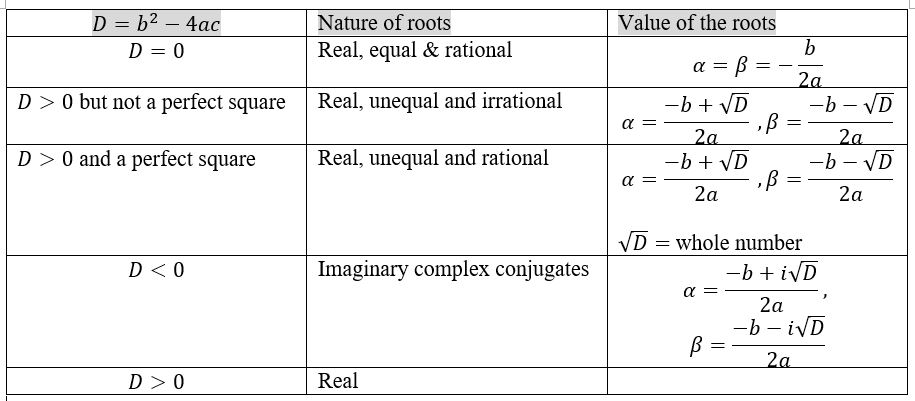
Transformation of equations:

Let  $\alpha$ and  $\beta$  are the roots of the equation  $a{x}^2+bx+c=0$

To find the equation whose roots are :

(i) Negative of the roots of the equation  $a{x}^2+bx+c=0$

The required roots are  $–\alpha$   and   $–\beta$ .

This can be obtained by substituting

$y=–\alpha =–x$     $\Rightarrow x=–y$

so,  $a{\left(–y\right)}^2+b\left(–y\right)+c=0$   $\Rightarrow a{y}^2–by+c=0$

or       $a{x}^2+bx+c=0$

(ii) Increased by  $h$  i.e.  $\alpha +h , \beta +h$

substituting  $y=\alpha +h=x+h$   $\Rightarrow x=y–h$

so,  $a{\left(y–h\right)}^2+b\left(y–h\right)+c=0$

$\Rightarrow a{y}^2+y\left(b–2ah\right)+\left(a{h}^2–bh+c\right)=0$

so the required equation is 

$a{x}^2+x\left(b–2ah\right)+\left(a{h}^2–bh+c\right)=0$

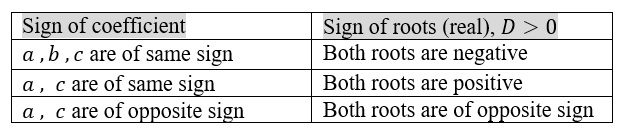
Sign of coefficient determining the sign of both real roots of $a{x}^2+bx+c=0$