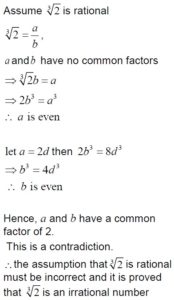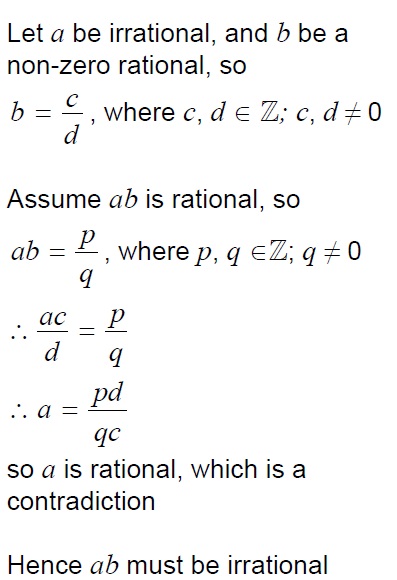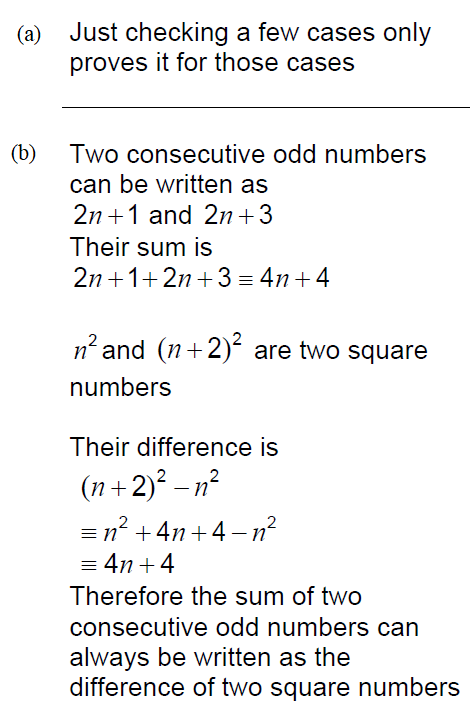Practice – Reasoning and Proof
1. Show that for all real numbers and
. (Triangle Inequality)
2. If and are not negative real numbers with , then .
3. For any real numbers and , show that .
4. Prove that if a, b, c are positive integers with a2 + b2 = c2 then either a or b is even.
5. Prove that is irrational. (prove by contradiction)
6. Prove that there does not exist a smallest positive real number.
7. If x , y , z are positive real numbers. Prove that x > z and y2 = xz implies that x > y > z.
8. Prove that if and are differentiable functions with , then either or .
9. Prove by contradiction that is an irrational number.
10. Prove that
n is a prime number greater than 5
has final digit 1.
11. A student argues that when a rational number is multiplied by an irrational number the result will always be an irrational number.
(a) Identify the rational number for which the student’s argument is not true.
(b) Prove that the student is right for all rational numbers other than the one you have identified in part (a).
12