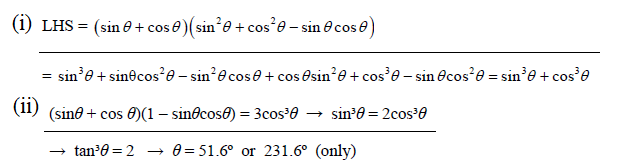Practice Questions – Trigonometric Identities and Equations

1. (i) Prove the identity  $\left(\sin \theta +\cos \theta \right)\left(1–\sin \theta \cos \theta \right)={\sin }^3\theta –{\cos }^3\theta$ .   [3 marks]

(ii) Hence solve the equation $\left(\sin \theta +\cos \theta \right)\left(1–\sin \theta \cos \theta \right)=3{\cos }^3\theta$ , for  $0°\le \theta \le 360°$ .   [3 marks]

2. (i) Express  $5 \cos \theta –2 \sin \theta$ in the form $R\cos \left(\theta +\alpha \right)$ , where $R>0$ and  $0<\alpha <\frac{\pi }{2}$ . Give the value of  $\alpha$ correct to 4 decimal places. [3 marks]

(ii) Using your answer from part (i), solve the equation  $5 cot\theta –4 \cos ec\theta =2$ for  $0<\theta <2\pi$ .   [5 marks]

3. (i) Prove the identity  $\frac{1+\cos \theta }{\sin \theta }+\frac{\sin \theta }{1+\cos \theta }=\frac{2}{\sin \theta }$ . [3 marks]

(ii) Hence solve the equation  $\frac{1+\cos \theta }{\sin \theta }+\frac{\sin \theta }{1+\cos \theta }=\frac{3}{\cos \theta }$ for  $0°\le \theta \le 360°$ . [4 marks]

4. (i) Express  $2 \cos \theta +\sqrt{5} \sin \theta$ in the form $R\cos \left(\theta –\alpha \right)$ where R > 0 and $0°<\alpha <90°$ , giving the value of  $\alpha$ correct to 2 decimal places. [3 marks]

(ii) Hence solve the equation  $2 \cos \theta +\sqrt{5} \sin \theta =1$ for  $0°<\theta <360°$ .   [4 marks]