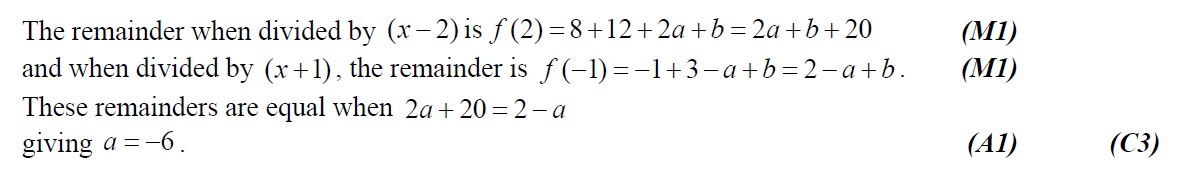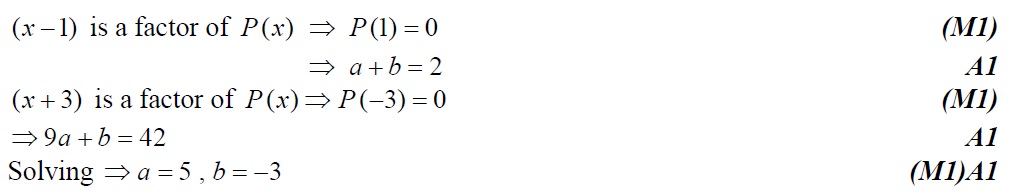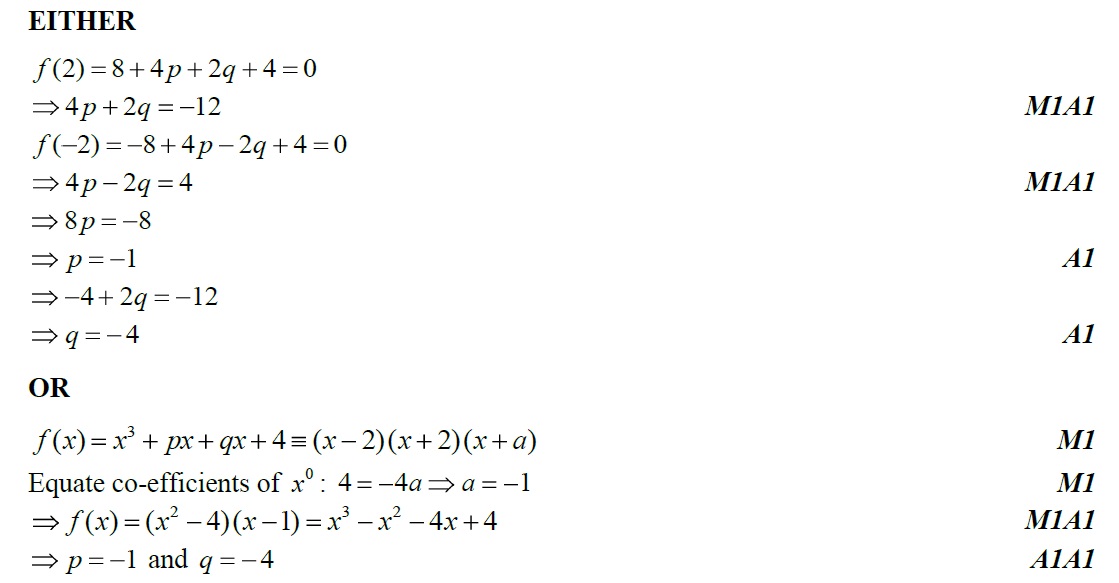IBDP Past Year Exam Questions – Polynomials

9709 March 5, 2020

Q1. [M99.P1]

When the function $f (x) = 6 x^{4} + 11 x^{2} - 22 x^{2} + a x + 6$ is divided by $(x + 1)$ the remainder is $- 20$ . Find the value of $a$ .[4]

Solution

Q2. [N99.P1]

The polynomial $p (x) = {(a x + b)}^{3}$ leaves a remainder of $- 1$ when divided by $(x + 1)$ , and a remainder of 27 when divided by $(x - 2)$ . Find the values of the real numbers $a$ and $b$ .[4]

Solution

Q3. [N01.P1]

The polynomial $f (x) = x^{3} + 3 x^{2} + a x + b$ leaves the same remainder when divided by $(x - 2)$ as when divided by $(x + 1)$ . Find the value of a.[3]

Solution

Q4. [N02.P1]

When the polynomial $x^{4} + a x + 3$ is divided by $(x - 1)$ , the remainder is 8. Find the value of $a$ . [6]

Solution

Q5. [M03.P1]

The polynomial $x^{3} + a x^{2} - 3 x + b$ is divisible by $(x - 2)$ and has a remainder 6 when divided by $(x + 1)$ . Find the value of $a$ and of $b$ .[6]

Solution

Q6. [M04.P1]

The polynomial $x^{2} - 4 x + 3$ is a factor of $x^{3} + (a - 4) x^{2} + (3 - 4 a) x + 3$ . Calculate the value of the constant $a$ . [6]

Solution

Q7. [N04.P1]

Consider $f (x) = x^{3} - 2 x^{2} - 5 x + k$ . Find the value of k if $(x + 2)$ is a factor of $f (x)$ . [6]

Solution

Q8. [N05.P1]

When the polynomial $P (x) = 4 x^{3} + p x^{2} + q x + 1$ is divided by $(x - 1)$ the remainder is $- 2$ . When $P (x)$ is divided by $(2 x - 1)$ the remainder is . Find the value of $p$ and of $q$ . [6]

Solution

Q9. [M06.P1]

The polynomial $P (x) = 2 x^{3} + a x^{2} - 4 x + b$ is divisible by $(x - 1)$ and by $(x + 3)$ . Find the value of $a$ and of $b$ .[6]

Solution

Q10. [N07.P1]

Given that $(x - 2)$ and $(x + 2)$ are factors of $f (x) = x^{3} + p x^{2} + q x + 4$ , find the value of $p$ and of $q$ . [6]

Solution

Q11. [M08.P1]

The polynomial $P (x) = x^{3} + a x^{2} + b x + 2$ is divisible by $(x + 1)$ and by $(x - 2)$ . Find the value of $a$ and of $b$ , where $a, b \in ℤ$ .[6]

Solution