Notes – Polynomials

A polynomial function, $p\left(x\right)$ , is an algebraic expression that takes the form   $p\left(x\right)=a_n{x}^n+a_{n–1}{x}^{n–1}+............+a_2{x}^2+a_{1}x+a_o , a_n\ne 0$

where the coefficients  $a_n , a_{n–1} , a_{n–2} , ............ , a_1 , a_0$ are real numbers, and the powers $n, n–1 , n–2 , ........$ are non- negative integers

The degree of a polynomial is the highest power of  $x$ in the expression.

SYNTHETIC DIVISION

Dividing a cubic polynomial  $p\left(x\right)=a_3{x}^3+a_2{x}^2+a_{1}x+a_0$ by a linear polynomial  $x–k$ .

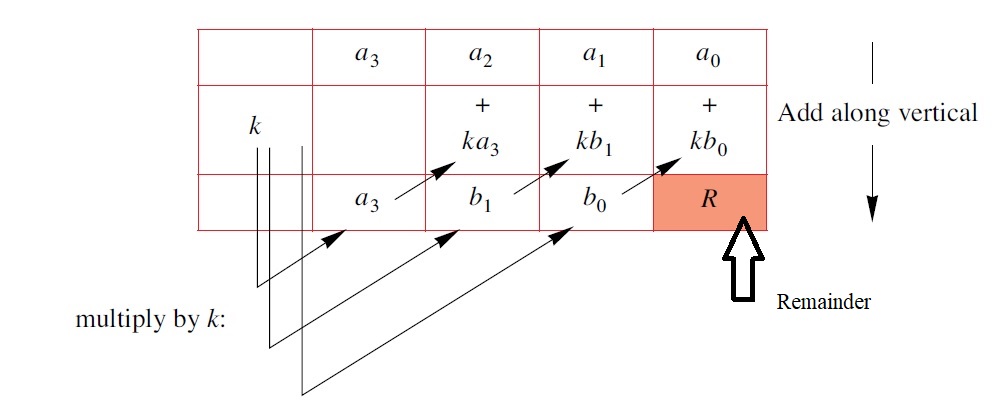
Quotient =  $a_3{x}^2+b_{1}x+b_o$   , Remainder = R

THE REMAINDER THEOREM

For any polynomial $p\left(x\right)$ , the remainder when divided by  $\left(x–\alpha \right)$ is $p\left(\alpha \right)$ .

Q. Find the remainder when  $3x^4+4x^2–2x+1$ is divided by  $x+2$ .

Remainder =  $p\left(–2\right)=3{\left(–2\right)}^4+4{\left(–2\right)}^2–2\left(–2\right)+1 = 69$

THE FACTOR THEOREM

$\left(x–\alpha \right)$ is a factor of  $p\left(x\right)$ if and only if  $p\left(\alpha \right)=0$ .

Q. Find the value of  $k$ if  $x–1$ is a factor of  $h\left(x\right)=x^3–k{x}^2+2x–1$ .

Since  $x–1$ is a factor of  $h\left(x\right)$ , so  $h\left(1\right)=0$

$\Rightarrow 1^3–k{\left(1\right)}^2+2\left(1\right)–1=0$

$\Rightarrow k=2$

Given a polynomial $a_n{x}^n+a_{n–1}{x}^{n–1}+............+a_2{x}^2+a_{1}x+a_o , a_n\ne 0$

has a factor $\left(px–q\right)$ if and only if  $p$ is a factor of  $a_n$ and  $q$ is a factor of  $a_0$ .

This result is useful in helping us guess potential factors of a given polynomial.

The polynomial: $h\left(x\right)=x^3+3x^2+6x+8$

can be factorised if we can find a factor (px – q) where p is a factor of 1 and q is a factor of 4.
Factors of 1 are 1 × 1 and factors of 4 are ±1 × ±4 and ±2 × ±2, so possible factors of $h\left(x\right)$  are  $\left(x\pm 1\right) , \left(x\pm 2\right)$ and $\left(x\pm 4\right)$ .

$x=–2$ , gives  $h\left(–2\right)=0$ . So, $\left(x+2\right)$ is one of the factors of  $h\left(x\right)$ .