Activity – Sequences and Series

1. To understand the concept of arithmetic sequence sketch the graph of some linear functions using some graphing software ( I used DESMOS). You will observe that when $n=1, 2, 3, .....$ the y-values will change increase/decrease with a constant number. Try to link it with the general term of an arithmetic sequence  $u_n=u_1+\left(n–1\right)d$ and draw the conclusion that the coefficient of n represents the common difference and also the gradient of the line. Here is an example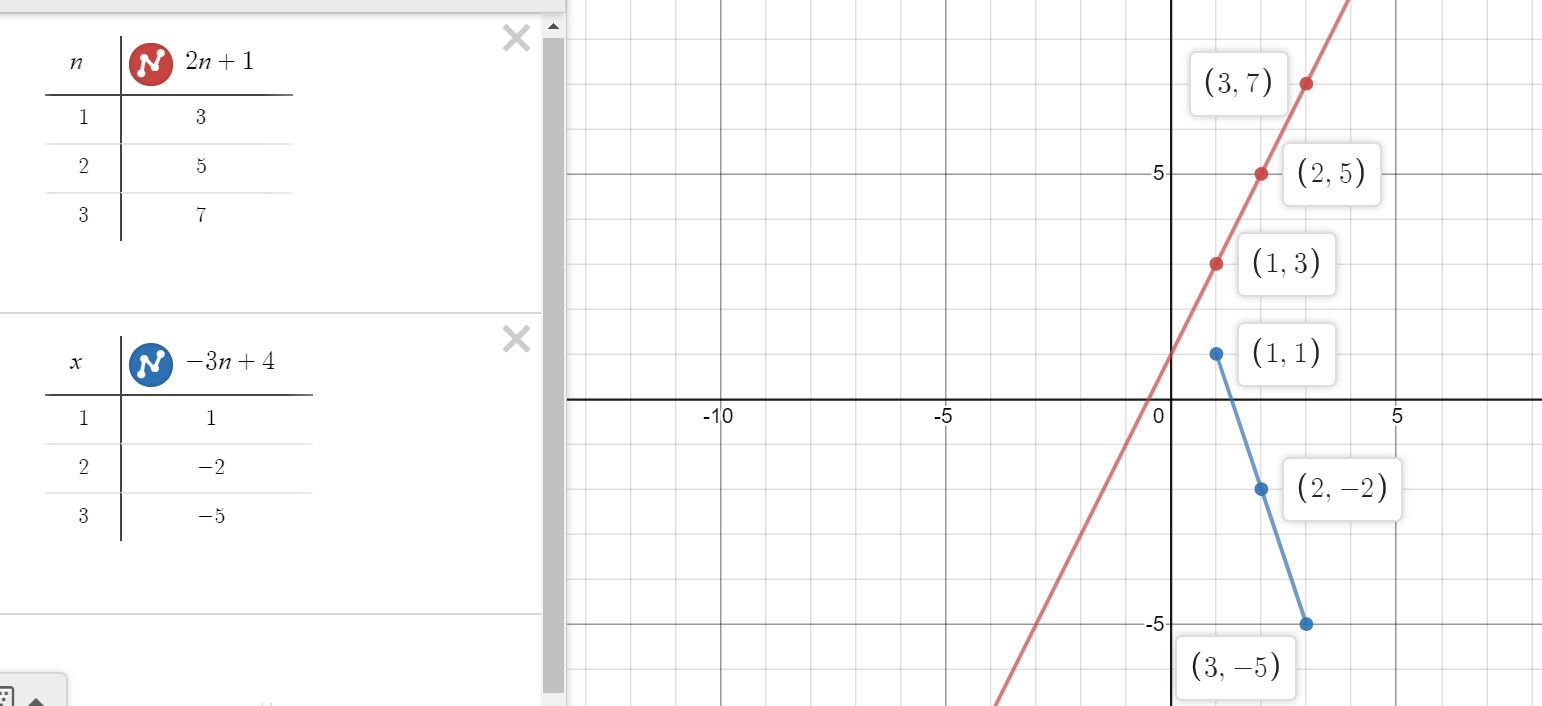

You can sketch exponential functions of the form  $y= a \times b^n$ to understand geometric series.

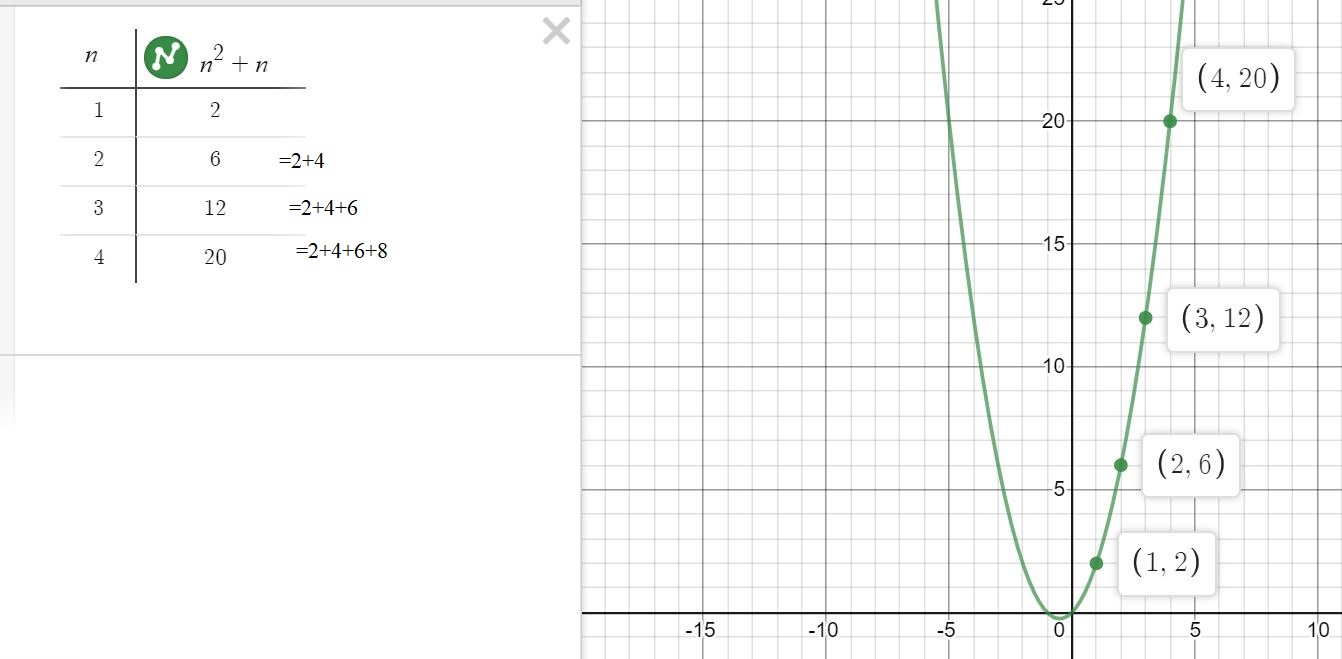
2. Sketch the graph of quadratics of the form  $y=a{n}^2+bn$ to understand the sum to n terms of an arithmetic series. e.g.