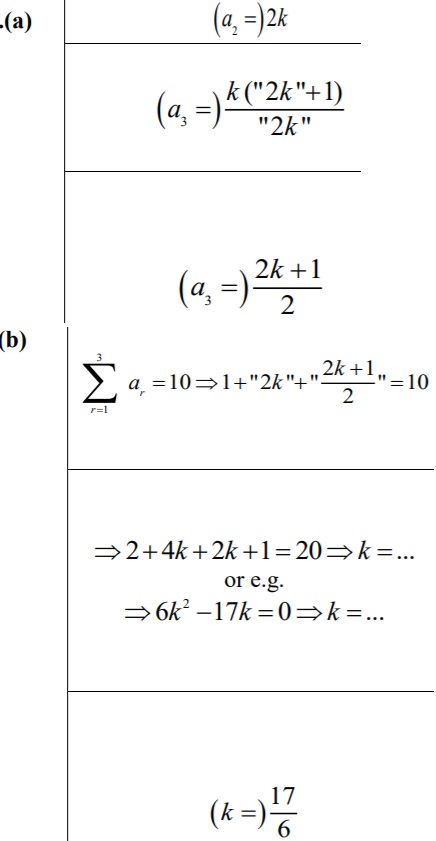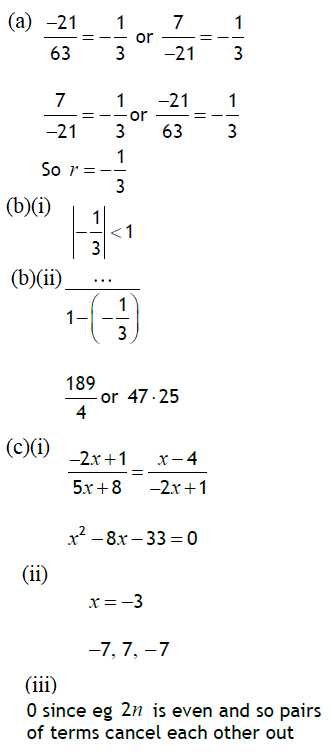Sequence and Series – Practice Questions

Q1. Suppose $\alpha , \beta$ are the roots of $x^2+kx+1=0$ and $\gamma , \delta$ are the roots of $x^2+x+k=0$ .

(a) if $\alpha , \beta , \gamma , \delta$ are in arithmetic sequence, then find the common difference of this arithmetic sequence in terms of $k$ ,

(b) if $\alpha , \beta , \gamma , \delta$ are in geometric sequence, then find the common ratio of this geometric sequence in terms of $k$ .

Q2. If the third term of a geometric sequence is 3 , then find the product of the first 5 terms?

Q3. The sum of an infinite geometric series with first term $x$ is equal to 3. Show that $–6<x<0$ .

Q4. Find the coefficient of $x^{49}$  in the polynomial $p\left(x\right)=(x–1)(x–2)(x–3)............(x–50)$ .

Q5. If $S_1 , S_2 , S_3 , ............ , S_n$  are the sum of infinite geometric series whose first terms are $2,3,4,..........(n–1)$  and whose common ratios are

$\frac{1}{3},\frac{1}{4},\frac{1}{5}, .........., \frac{1}{n}$  respectively then find the value of  $S_1 + S_2+S_3+.............+S_{2n}$ .

Q6. Find  $a$ in terms of  $c$  if  are in arithmetic sequence.

Q7. Find the value of $x$ if  $\ln (3^x–1), \ln (3^x+1), \ln (3^{x+1}–1)$  are in arithmetic sequence.

Q8. Find the sum to  $n$  terms of the series:  $\frac{3}{2}+\frac{5}{4}+\frac{9}{8}+\frac{17}{16}+...........$

Q9.  $\ln a–\ln 2b , \ln 2b–\ln 3c , \ln 3c–\ln a$  are in arithmetic sequence. If  $a , b , c$  

are in geometric sequence, show that  $a=\frac{9c}{4}$ .

Q10. Two arithmetic sequences have the sum of their $n$

terms in the ratio  $3n:(2n–1)$  . Find the ratio of their 23^rd terms.

Q11. Show that the sum to $n$ terms of the series  $2+\frac{8}{3}+\frac{26}{9}+\frac{80}{27}+\frac{242}{81}+.........$  is  $3n–\frac{3}{2}+\frac{1}{2\times 3^{n–1}}$  .

Q12. If  $S=\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+............\infty$  , then find the value of ${\left(0.5\right)}^{{\log }_3\left(S\right)}$  .

Q13. Find the values of $a , b$  and $c$ if

$\frac{x^{11}–1}{x–1}=1+ax+b{x}^2+c{x}^3+............+x^{10}$   where  $a, b, c \in \mathrm{ℝ}$ .

Q14. If  $a, b$ and  $c$  are the  $m^{th}, n^{th}$ and $p^{th}$  terms respectively of an arithmetic sequence and also a geometric sequence, then show that the value of $a^{\left(b–c\right)}{b}^{\left(c–a\right)}{c}^{\left(a–b\right)}$  is equal to 1.

Q15. If $x, y, z$  are respectively the  $p^{th}, q^{th}, r^{th}$ of a geometric sequence, then show that the value of $\left(q–r\right)\ln x+\left(r–p\right)\ln y+\left(p–q\right)\ln z$  is equal to zero.

Q16. (a) A geometric progression has a second term of 12 and a sum to infinity of 54. Find the possible values of the first term of the progression. [4 marks]

(b) The $n$ th term of a progression is $p+qn$ , where  $p$ and  $q$ are constants, and  $S_n$ is the sum of the first  $n$ terms.
(i) Find an expression, in terms of  $p, q$ and $n$ , for $S_n$ . [3 marks]

(ii) Given that $S_4=40$ and $S_6=72$ , find the values of  $p$ and $q$ . [2 marks]

Q17. A sequence  $a_1 , a_{2 }, a_3 ,.....$ is defined by

$$\begin{gathered} a_1=1 \\ {a}_{n+1}=\frac{k\left(a_n+1\right)}{a_n}, n\ge 1 \end{gathered}$$

where $k$  is a positive constant.
(a) Write down expressions for  $a_2$ and $a_3$ in terms of $k$ , giving your answers in their simplest form. (3 marks)

Given that  $\sum _{r=1}^3{a}_r=10$
(b) find an exact value for $k$ .  (3 marks)

Q18. A company, which is making 140 bicycles each week, plans to increase its production.
The number of bicycles produced is to be increased by d each week, starting from 140 in week 1, to 140 + d in week 2, to 140 + 2d in week 3 and so on, until the company is producing 206 in week 12.
(a) Find the value of d.  (2 marks)
After week 12 the company plans to continue making 206 bicycles each week.
(b) Find the total number of bicycles that would be made in the first 52 weeks starting from and including week 1. (5 marks)

Q19. The first three terms of a geometric sequence are $7k – 5, 5k – 7, 2k + 10$ where  $k$ is a constant.
(a) Show that $11k^2 – 130k + 99 = 0$    (4 marks)
Given that  $k$ is not an integer,
(b) show that  $k=\frac{9}{11}$   (2 marks)
For this value of $k$ ,
(c) (i) evaluate the fourth term of the sequence, giving your answer as an exact fraction,
(ii) evaluate the sum of the first ten terms of the sequence. (6 marks)

Q20. A sequence $u_1 , u_2 , u_3 , .......$ is defined by $u_1=7$ , $u_{n+1}=u_n+15$ .
The sum of the first  $n$ terms of this sequence is denoted by $S_n$ . The terms of a second sequence $v_1 ,v_2 , v_3 ,......$  form a geometric progression with first term 1.2 and common ratio 1.2.
(i) Show that $u_3 + v_3 = 38.728$ .  [2 marks]
(ii) Show that $S_{70} = 36 715$ .        [3 marks]
(iii) Find the largest value of  $p$ such that $v_p< S_{70}$ .     [3 marks]
(iv) Find the largest value of $q$ such that $S_q< v_{70}$ .       [4 marks]

Q21. The first three terms of a sequence are given by                                                                  $5x+8, –2x+1, x–4$
(a) When $x=11$ , show that the first three terms form the start of a geometric sequence, and state the value of the common ratio.

(b) Given that the entire sequence is geometric for  $x=11$
        (i) state why the associated series has a sum to infinity
        (ii) calculate this sum to infinity.

(c) There is a second value for  $x$ that also gives a geometric sequence.
For this second sequence
             (i) show that  $x^2–8x–33=0$
             (ii) find the first three terms
             (iii) state the value of  $S_{2n}$ and justify your answer.

22. A geometric sequence has first term 80 and common ratio  $\frac{1}{3}$ .
(a) For this sequence, calculate:
(i) the  $7^{th}$ term;      [2 marks]
(ii) the sum to infinity of the associated geometric series.    [2 marks]
The first term of this geometric sequence is equal to the first term of an arithmetic sequence.
The sum of the first five terms of this arithmetic sequence is 240.
(b) (i) Find the common difference of this sequence.    [2 marks]
(ii) Write down and simplify an expression for the nth term.    [1 mark]
Let  $S_n$ represent the sum of the first  $n$ terms of this arithmetic sequence.
(c) Find the values of  $n$ for which $S_n=144$ .  [3 marks]

23. (a) Three consecutive terms in an arithmetic sequence are  $3e^{–p} , 5 , 3e^p$ . Find the possible values of $p$ . Give your answers in an exact form.

(b) Prove that there is no possible value of q for which  $3e^{–q} , 5 , 3e^q$ are consecutive terms of a geometric sequence.